Три закона Кеплера

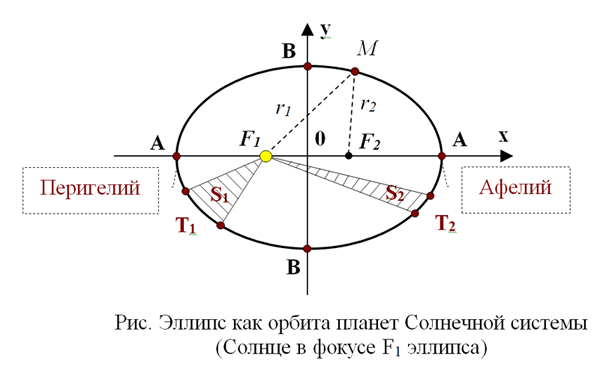
1) каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце (эллипс, или плоская овальная кривая 2-го порядка - множество точек М, сумма расстояний которых от двух данных точек F₁и F₂ - фокусов эллипса - постоянна и равна длине большой оси эллипса: r₁+r₂=2a, где r₁,r₂ - расстояния до точки М соответственно от первого и второго фокусов, а- большая полуось, см. рис.; в прямоугольной системе координат уравнение эллипса имеет вид: x²/a²+ y²/b²=1, b²=a²-c², где b - малая полуось, с - модуль абсциссы фокусов F₁ , F₂; очевидно, что АА=2а, ВВ=2b,  F₁F₂=2с;  при а=b фокусы совпадают, с=0, и эллипс превращается в окружность; форма или ”вытянутость” эллипса определяется его эксцентриситетом e - отношением расстояния между фокусами к  длине большой оси: e=2с/2а=с/а<1, для окружностиe=0; на эллипсе, как орбите небесного тела обращающегося вокруг Солнца, ближайшая к Солнцу точка орбитыэтого тела называется перигелием - от греч. peri вокруг, около, возле + heliosсолнце, а наиболее удаленная точка - афелием - от греч. apoвдали + helios; для Земли, например, расстояние от центра планеты до центра Солнца в перигелии приблизительно равно 147,1 млн. км, в афелии ~ 152,1 млн. км, а среднее (147,1+152,1)/2≈149,6 млн. км = 1 а.е.; степень вытянутости орбит у разных планет Солнечной системы различна и для Земли, например, составляет e=(152,1-147,1)/(152,1+147,1)≈0,017, т.е очень мала - орбита Земли мало отличается от окружности; для Марса e= 0,093 при среднем расстоянии до Солнца 1,524 а.е.≈228 млн.км, а самая вытянутая орбита у Меркурия - e= 0,206 при среднем расстоянии планеты до звезды 0,387 а.е.≈57,9 млн. км);

2) каждая планета движется в плоскости, проходящей через центр Солнца, причем площадь секторов орбиты, описанная радиус-вектором планеты, изменяется пропорционально времени, т.е. S₁/S₂=T₁/T₂, где S₁,S₂ – площади двух различных секторов, а T₁,T₂- времена прохождения планетой орбиты по соответствующим секторам (см.  рис.). При T₁=T₂ будет и S₁=S₂, а так как при равных площадях секторов в эллипсе путь, пройденный планетой в секторе с большим радиусом - планета дальше от Солнца - будет меньше, то, следовательно, по мере приближения планеты к Солнцу, когда радиус-вектор уменьшается, она будет проходить в одно и то же время по своей орбите больший путь, т.е. скорость движения планеты по орбите не остается постоянной, как при равномерном движении, а увеличивается - планета движется с положительным ускорением. Соответственно, при удалении планеты от Солнца ее орбитальная скорость уменьшается - планета движется с отрицательным ускорением, или замедляет свой ход. Например, для Марса орбитальная скорость в перигелии равна 26,5 км/с, а в афелии - 22 км/с при средней скорости 24,1 км/с, адля Земли средняя скорость равна 29,8 км/с и изменяется незначительно из-за малого эксцентриситета ее орбиты. У некоторых комет, обращающихся вокруг Солнца орбита настолько вытянута, что вблизи перигелия их скорость доходит до 500 км/с, а в афелии падает до 1 см/с;

3) квадраты времен обращения планеты вокруг Солнца относятся как кубы их средних расстояний от Солнца, т.е. (Tобр₁/Tобр₂)²= (r_ср1/r_ср2)³, где Tобр₁,Tобр₂ - времена обращения первой и второй выбранных планет, r_ср1,r_ср2- средние расстояния этих двух планет от Солнца. Если в качестве одной из сравниваемых планет выбрать Землю с известными r_ср1=1 а.е. и Tобр₁=365,25 суток=1 год, то измерив Tобр₂ второй планеты, можно по формуле r_ср2= (Tобр₂²)^1/3 определить ее среднее расстояние от Солнца. Например, для Марса Tобр₂=1,88 земных годаи по формуле получим r_ср2=1,52 а.е.

Позже эти законы получили свое физическое объяснение в механике Ньютона, который доказал, что все они являются следствием закона всемирного тяготения. Он их уточнил и, в частности показал, что движение небесных тел может происходить (в зависимости от их масс, расстояний и скоростей) не только по эллипсу, но и по гиперболе и параболе.