1. Большой взрыв, время ≾0

Если ориентироваться на работу Г.А. Гамова и его сотрудников по исследованию теории БВ[i], то область температур, в пределах которой могло длительно существовать пространство Ничто, лежит в значениях температуры в границах ≾0 К.

Наиболее всего по современным физическим теориям к кристаллам несамостоятельных тел и ПНВЧ подходят квазичастицы, исследование которых будет в соответствующей части Физики. Также мы отметим, что согласно теории БВ, к такому взрыву могли привести гипотетические элементы с бесконечно большой потенциальной энергией собственного абсолютного покоя, так и с бесконечно большой кинетической энергией движения – Духа, последний согласуется с понятием «абсолютный дух» как у Гегеля так и «λόγος» у Хайдеггера[ii]). В настоящей гипотезе это алмаз и жидкий углерод с металлической структурой.

При переходе же в метастабильное конечное существование Наличного мира и затем в природу, мы имеем как результат их взаимодействия – «субъекты реального мира», а, от Духа, еще и «субъективный дух», как его единичное инобытие.

Учитывая то обстоятельство, что элементы реального непрерывного пространства постоянно находятся во взаимодействии, мы для описания их движения можем применять понятия и математический аппарат классической механики и теории упругости.

Количество движения и его моменты.

Количество движения, является в механике универсальной мерой действия и поступательного движения материальных тел. Как мера движения оно отражает Iи II законы механики, описывающие движение и взаимодействие материальных тел. Как мера действия оно отражает характеристики полей физических, характеризуя меру их действия между собой и на окружающие материальные тела. 

В данной работе, в соответствии с Нетера теоремой[iii], являющейся фундаментальной теоремой физики, устанавливающей связь между свойствами симметрии физической системы и законами сохранения,

«Мера механического движения, равная для материальной точки произведению её массы m на скорость υ. Количество движения mυ– величина векторная, направленная так же, как скорость точки»[iv]. Рассматривая в этом аспекте движения и взаимодействие тел при взаимодействии, отметим следующее, мы вместо понятия силы используем понятия момента действия[v] (M) и момента количества движения К, которые отражают меры действия тел друг на друга и их последующие движения.

Если одно тело в поступательном движении взаимодействуют (соударяются) в точке Oс телом находящемся в покое по линии симметрии. Согласно II закону Ньютона о постоянстве количества движения можно записать m₁υ₁ = I, где I – импульс силы, в дальнейшем импульс действия[vi](ИД) который имеет первое тело до взаимодействия со вторым. После взаимодействия ИД перераспределяется между двумя телами –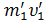= m₂υ₂= I′(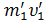+ m₂υ₂ = I). Вектора [I] и [I′] будут направлены по оси взаимодействия, совпадающей с осями симметрии обоих тел (рис. 1, а).

Тот же вариант взаимодействия, но, когда ИД не совпадает с осью симметрии покоящегося тела. Для упрощения мы рассматриваем покоящееся тело шарообразной формы, когда точка взаимодействия тел происходят на расстоянии радиуса (r) в точке B′. При этом оба тела получают дополнительно к поступательным вращательные движения, основой которого является момент количества движения (МКД) – K₁, в который частично перейдет энергия движения ИД.

МКД для покоящегося тела относительно центра O можно вычислить: По модулю K_О = I·h, где h– плечо т. е. длина перпендикуляра, опущенного из центра Oна линию действия I). Или как векторное произведение K_О = [Ir] (рис. 1. a).

МКД относительно оси величина алгебраическая, равная проекции на эту ось K₁ относительно точки O или же численной величине момента проекции K_1xyмомента K₁ на плоскость xy, перпендикулярную оси z, взятого относительно точки O. Вращение тел с незакрепленной осью симметрии согласно момента пары сил[vii] (рис. 1, б) приведет к формированию у него момента действия (МД), направление которого будет перпендикулярно плоскости вращения. Для покоящегося тела МД M_O2 ⊥ AA′B′B, угол γ₂ = arctgh/2πr[viii] и равен M_O2 = M_Ozcosγ₂ = ±K_xyh₁. Знак плюс в последнем выражении берётся, когда поворот МКД K_xy с положит, конца оси z виден против хода часовой стрелки (тоже в правой системе) (рис. 1, б).

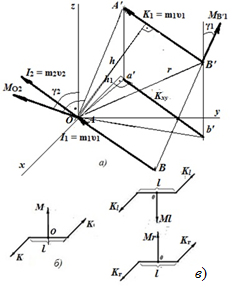
Рис. 1. Схемы: a) действие на тело I = mυ и момента количества движения (К_O= mυ·h); б) формирование МД при действии МКД в) разложение K_O на пару взаимно-противоположных моментов количества движения – правого и левого (R, L);

Таким образом, МД M_O2 и полученный ИД I₂ = m₂υ₂ начинают формировать поступательно-вращательное количество движения (КД) Q₂ покоящегося тела, направление которого буде определяться векторной суммой Q₂ = [M_O2] + [I₂].

Составными движениями первого (не шарового) тела после взаимодействия также являются и поступательные, и вращательные. Но результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений[ix], в результате общее направление первого тела будет определяться также векторной суммой КД Q₁ = [M_B′1] + [I₁], где I₁= m₁υ₁ – ИД тела, сформированный после взаимодействия (рис. 1, а).

Если система сил имеет равнодействующую, то её момент вычисляется по Вариньона теореме[1].

Разрушение пространства Ничто.

Согласно нашей гипотезе ПНВЧ из жидкого углерода при высоких температурах может принять металлическую структуру, а кристалл алмаза распадается на два изотопа углерода ¹²C↔ ¹³C, вращающихся одни в правой, другой в левой системе. Это происходит под действием МД ПНВЧ Q = 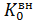+ mυ² (рис. 2). В этом момент начинается действие их момента количества движения –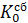 в которые перешла часть энергии МД ПНВЧ.  Изотопы мгновенно начали неупорядоченное собственное вращение[x] ω^сб, которое можно трактовать как высвобождение или выброс энергии.

Это не противоречит теории взрыва, когда участвующие в нем разрушающиеся элементы освобождают «большого количества энергии в ограниченном объёме за короткий промежуток времени. В результате взрыва вещество, заполняющее объём, в котором происходит освобождение энергии, превращается в сильно нагретый газ с очень высоким давлением. Этот газ с большой силой воздействует на окружающую среду, вызывая её движение. Взрыв в твёрдой среде сопровождается её разрушением и дроблением...»[xi] и переходом большей части твердой среды в газообразную. Данный процесс подходит под описания процесса сублимации как «переход вещества из кристаллического состояния непосредственно (без плавления) в газообразное»[2], т. е. с выделением энергии. В этот момент у вращающихся элементов отсутствует какое-либо стремление и возможность, как к упорядочению своего движения.

В замкнутом пространстве БВ происходит резкое повышение температуры и давления, что приводит к образованию по границе распада фронта ударной волны. Давление, которое создаётся при распространении данной волны в твёрдо-газообразной смеси составляет в тысячи атмосфер.[xii]

Поэтому движение ПНВЧ с металлической структурой получает дополнительную энергию движения уже под действием собственного вращения изотопов углерода. Металлическая структура ПНВЧ при этом не изменяется. Его течение подобно жидкой плёнки не связано с плавлением его структуры, а вызвано чрезвычайно высокой механической нагрузкой.[xiii] Таким образом, он подобно «ножу» разрезает кристаллы пространства ПНВЧ. Можно предполагать, что разрез будет идти по некоторому равному по величине энергетическому разлому. Наиболее возможно, что он проходит по линии МКД, т. е. разделяет кристалл на два равных изотопа с максимально возможным равным по величине, но противоположным по направлению собственным вращением как правая и левая системы пары сил (рис. 1, в).

Это непременное условие предполагает, что при некоторых внешних условиях должно произойти восстановления пары элементов обратно в кристалл. Таким образом, моменты распада кристаллов и их восстановление можно рассматривать как критическое состояние материи. А при «приближении к критическому состоянию физические свойства вещества резко изменяются: теоретически неограниченно возрастает теплоёмкость и восприимчивость системы к внешним воздействиям»[xiv]. В двухкомпонентных системах характерные для критического состояния явления наблюдаются в критических точках равновесия. Эти точки являются температурными границами области расслаивания (фазовых переходов) на фазы различного состава. Такой способностью обладают некоторые и твёрдые растворы,[xv] и, следовательно, сам единичный кристалл можно рассматривать как твердый раствор двух изотопов газообразного или жидкого углерода.

Это не противоречит тому, что если «кристалл принадлежит к классу, содержащему лишь простые оси симметрии (но не содержащему плоскостей, центра симметрии или инверсионных осей), то он может кристаллизоваться в зеркально равных формах. Это явление называют энантиоморфизмом[3], а соответствующие энантиоморфные формы – «правой» и «левой»»[xvi] Поскольку в момент БВ изотопы углерода находятся в газообразном состоянии, то корректно будет предположить, что в момент распада энергия КД ПНВЧ полностью переходит МКД 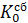данных изотопов (рис. 2). ИД они самостоятельно сформировать не могут в виду практически нулевой массы m = 0.

Высокая механическая нагрузка воздействия ПНВЧ на несамостоятельные тела, способствовала, распаду их элементов по всей его внешней границе по мере «продвижения» в пространстве Ничто.

Полярность.

«Внедрение» ПНВЧ в тело кристалла создает как внешнее воздействие перпендикулярные составляющие импульса действия m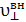, под действием которого начинается поступательно-вращательное движение газообразных элементов в противоположные стороны со скоростью υ^сб.

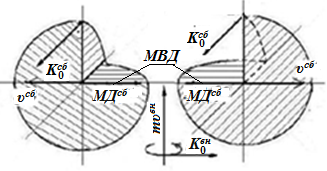
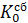Рис. 2. Векторы МКД  (правой и левой системы) и ±МД изотопов углерода, в результате воздействия потока внешних частиц.

В этот момент, как отстаивание материей свое в-себе-инобытие как возврат в кристалл начинают формирование направленные навстречу их ±МД^сб правой и левой систем. Для удобства изложения суммарное одновременной действие МД будем обозначать вместе как моменты взаимодействия (МВД) элементов правой и левой систем вращения (рис. 1. в, 2), а сами элементы как крайние единичные противоположности (КЕП).

Учитывая факт того, что потенциальная энергия покоя элементов несамостоятельных тел равна энергии МД ПНВЧ Q = mυ^вн + 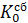, то можно сделать вывод, что энергия собственного вращения КЕП – ω^сб ⩾ ½ ω_max. Знак ⩾ показывает, что в ω^сб перешла и часть энергии поступательного движения потока неких внешних частиц – mυ^вн (рис. 2, а). Следовательно, их МД^сб и единый МВД будут отражать потенциальную энергию их действия или взаимодействия.

С точки зрения философии, МВД отражают стремление материи перейти из состояния для-себя-бытие к состоянию в-себе-бытие, т. е.возврату в кристалл. Данное взаимодействие полярных КЕП подпадает под понятие полярности. Это согласуется с позицией Гегеля: «В физике много говорилось о полярности; это понятие есть великий шаг вперед физики в ее метафизике, ибо мысль о полярности является не чем иным, как определением соотношения необходимости между двумя различными, которые являются единым, поскольку с полаганием одного непременно оказывается положенным также и другое. Эта полярность ограничивается лишь противоположностью, но посредством противоположности полагается, как единство, также и возвращение из противоположности, и это есть третье. В этом состоит тот плюс, который заключает в себе необходимость понятия по сравнению с полярностью»[xvii]. Таким образом, полярные КЕП отражают материю в состоянии в-себе-бытие, которое не есть уже «чистое бытие», поскольку уже не блокируются мыслью, а контролируются Идеей.

По нашей гипотезе, происходит изменение беспорядочного вращения двух изотопов ¹²C↔ ¹³C[xviii], с формированием у них полярных направленных навстречу друг другу МД или общего МВД.

Поляризация Iи II.  

Установившаяся полярность характеризуется двумя понятиями «поляризации»[xix]. Первое, – когда «поляризацию» связывают с наличием у полярных КЕП собственного синхронного вращение (ω_КЕП) вокруг оси МВД, которые отражают направленные в одну сторону, но формируемые в правой и левой системах их МКД – 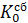. Второе, – когда под понятием «поляризация» понимают наличия у них МД^сб, которые в виде МВД отражают взаимное стремление КЕП к возврату в состояние кристалла несамостоятельного тела. Первое значение мы обозначим понятием поляризация I, а второе –поляризация II.

Таким образом, поляризация I характеризует потенциальную энергию собственного вращения КЕП как ±МКД^сб, а поляризация II характеризует их потенциальную энергию взаимодействия векторов ±МД^сб. 

Условно, для противоположно поляризованных КЕП в бытийном понимании вводятся понятия положительной и отрицательной поляризации. При этом, примем положение, что поляризация IIв правой системе будет положительной и в левой системе отрицательной (см. рис. 2, 3. б, в). В левой системе координат поляризация данных элементов поменяет знаки.

Крайние единичные противоположности.

Распад на две КЕП не противоречит древнегреческим философам в том, что сущностью Природы, когда она переходит в качество, является распад ее на «две противоположности»[xx].

Под термином «распад» в данном случае будем понимать процесс перехода массы инертной материи (потенциальная энергия покоя) кристалла несамостоятельного тела, в абсолютную энергию внутреннего собственного вращения ω^сб КЕП. Таким образом, в КЕП, материя предстает нам как материя в состоянии для-себя-бытие.

Это согласуется с логикой Аристотеля, который утверждал, говоря о сущности, что «нельзя говорить о движении движения, как и о возникновении возникновения, и вообще – об изменении изменения». Ибо, например, «если возникновение <само по себе> когда-нибудь возникало, то возникало и возникающее, а потому возникающего непосредственно еще не было, но было уже нечто становящееся <этим> возникающим. И оно <тоже> когда-нибудь возникало, так что тогда оно еще не было таким (становящимся). (5) А, так как у бесконечных <рядов> не бывает чего-либо первого, тогда <при нашем предположении> <такого> первого не будет, а, следовательно, <не будет> и того, что идет за ним. Поэтому <здесь> нельзя говорить ни о возникновении чего-либо, ни о движении, ни об изменении...»[xxi].

В этом состоит и проблема перенормируемости в квантовой теории поля, когда «в ней появлялись бессмысленные бесконечно большие значения (расходимости) для некоторых физических величин и отсутствовало понимание того, что же с ними делать»[xxii].

В «Метафизике» раскрывая понятие «единого», Аристотель связывает с ним, «непрерывное – либо непрерывное вообще, либо (и это – главным образом) – то, что является непрерывным по природе, а не через соприкосновение или связь (да и из этого <всего> в большей мере и скорее надо считать единым то, движение, что нераздельнее и более просто)».

И далее Аристотель говорит: – «поэтому ясно, что, если чему-нибудь принадлежит от природы в первичном роде движения первичный его вид (я имею в виду движение пространственное и здесь <выделяю специально> движение круговое), в таком случае – это есть первая единая величина...»[xxiii].

В данной работе такой первой единой величиной, в реальном пространстве, по моему мнению, является ω^сб КЕП, поскольку, характеризуя понятие «бесконечная величина», исходим из раскрытия понятия бесконечности, как максимально возможное, даваемое Аристотелем[xxiv].

Следуя за Гегелем, можно утверждать, что в формирующееся «противоположение существует лишь как противоположение; оно лишено опоры и представляет собой лишь внутреннее крушение. Для того чтобы оно носило характер воодушевленного противоположения, требуется наличие среднего члена, который удерживал бы раздельно её[4] полярные члены и являлся бы их носителем»[xxv]. В начальный момент БВ таким «средним членом», удерживающим в раздельности противоположности, является ПНВЧ, как пространство бесконечное множества вращающихся кристаллов.

Таким образом, первые элементы абстрактного реального пространства есть результат взаимодействия Бытия и Небытия. И абстракция для-себя-бытия материи получает здесь свое некое «надлежащее место», в начале процесса БВ представляя собой случайность, но также и внутреннюю необходимость процесса развития Разума.

Абсолютная свобода – для-себя-бытие материи.

Таким образом, идеальность сущности для-себя-бытия материи в максимально возможном собственном вращении ω^сб КЕП, проявляется абстрактной непрерывностью элементов реальных пространств. Если бы можно было выделить из него единичное место, в котором как идеальные присутствуют вращающиеся синхронно единичные однополярные КЕП, то это и будет единичное место реального пространства. Реального, потому что данное вращательное движение уже можно связать с некой длительностью, связанной аннигиляцией КЕП в целый кристалл. Это то, что добивалась материя, – абсолютное свобода «для-себя-бытия» в своем длительном бытии.

Инвариантность КЕП

В то время полярные КЕП с максимально возможными взаимно противоположными МД^сб и 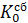, становятся субъектами взаимодействия. При этом как объекты они обладают свойством абсолютной инвариантности. А последняя «тесно связана с имеющими большое значение сохранения законами[5]… приводит к закону сохранения импульса; равноправие всех направлений в пространстве (изотропия пространства) – к закону сохранения момента количества движения; … – к закону сохранения энергии и т. д…»[xxvi].

Притяжение и Отталкивание.

Потенциальная энергия данного взаимодействия КЕП при невозможности реализации ими поступательного движения можно рассматривать как «притяжение» КЕП разной полярности. Это притяжение сдерживается ПНВЧ, поддерживая длительность существования для-себя-бытия материи, предотвращая их аннигиляцию.

Взаимодействия однополярных КЕП реализуемое как отталкивание проявляется в следующих трех вариантах (рис. 3).

Рис. 3. Взаимодействие КЕП одной поляризацией.

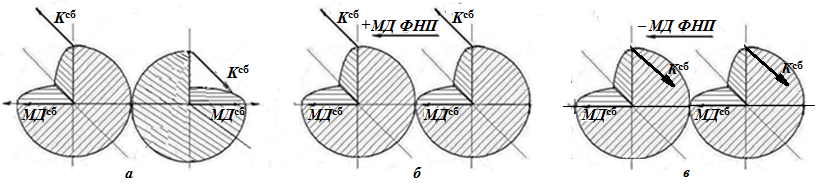
Первый вариант предполагает, что КЕП рассматриваются как самостоятельные элементы со своей системой координат. В этом случае поляризация II как МД^сб правой системы будут направлены в противоположные стороны (рис 3, а), т. е. однополярные КЕП отталкиваются. Во втором, – они формируются как несчетное множество в метастабильных пространствах как поляризованное поле, где поляризация II в качестве вектора МД^сб отражает направление её действия в правой системе. И в третьем, – левой системы (рис. 3, б, в). Поляризация I, во всех трех случаях отражает вектор собственного вращения ω^сб, либо КЕП, либо пространства как единого тела, которое в физике часто определяют термином «спиновая упорядоченность»[xxvii]

Поскольку во всех трех вариантах взаимодействие основано на отталкивании однополярных КЕП, то можно предположить, что именно такие взаимодействия Гегель называет «формальное» отталкивание»[xxviii].

По нашей гипотезе, процесс БВ отражает критическое состояние материи, где образования КЕП идет скачкообразно, а их множества – лавинообразно. В таком случае, величины их МД^сб и 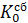мгновенно вырастают до максимально возможных величин.

Здесь «материя есть нераздельно то и другое, и она есть вместе с тем отрицательное единство этих моментов, единичность, но единичность пока еще отличная от непосредственной внеположности материи и поэтому сама еще не положенная как материальная; она есть идеальная единичность, центр, тяжесть».[xxix]

Функциональные пространства

Потенциал, упорядоченное вращение, вектор.

Полярность, определяющаяся собственным вращением КЕП можно определить, как мобилизационные источники для возвращения полярных КЕП в элемент пространства Ничто, что подходит под определения потенциала[6]. Следовательно, формирующиеся из КЕП два полярных пространства реального мира можно определить, как потенциальные статические поля полярностей Iи II. Статические потенциалы каждого полярного пространства КЕПa(x, y, z)  есть скалярная функция такая, что a = gradu, т. е. a_x= , a_y= , a_z= , где a_x, a_н, a_я, – компоненты пространства a в системе декартовых координат 0xyz»[xxx]. Потенциальная функция[xxxi] полярных элементов таких пространств будет отражать энергию необходимую для полной аннигиляции КЕП в кристалл пространства Ничто. Таким образом, данные формирующиеся пространства представляют собой непрерывные функции полярно-статистических полей. Это позволяет классифицировать их как «функциональные пространства»[7] (ФНП).

Потенциальная энергия в виде МД пары сил (рис. 1, в), как результат взаимодействия векторов ±МД полярных КЕП, действует по оси МВД. Максимальный вектор МВД будет если оси их векторов МД совпадают. Такое возможно для КЕП в несвязанном состоянии, как, например, при их образовании в процессе БВ, когда υ^сб и MД при этом способствует формированию их упорядоченному вращению. Так как величины ±МД и КЕП лежат в максимально больших значениях, то мы можем обозначить их только в виде векторов (от лат. vector, буквально – несущий, перевозящий), в геометрическом смысле – направленный отрезок, у которого указаны начало, называемое также точкой приложения и конец[xxxii].

Вектор поляризации I ФНП позволяет ввести понятие – вихрь векторного поля, – векторная характеристика «вращательной составляющей» данного пространства[xxxiii].

Таким образом, физические элементы функций, задающих поля ФНП, отражаются только векторами МД и. Поэтому основным математическим аппаратом при изучении данных пространств является векторное исчисление[8].

Космологические теории ФНП

Космологические теории разных эпох (а часто и относящиеся и к одной и той же эпохе) существенно различаются в зависимости от того, какие физические принципы и законы принимаются в качестве достаточно универсальных и кладутся в основу космологии. Степень универсальности принципов и законов не может быть проверена непосредственным путём, но построенные на их основе модели должны допускать проверку; для наблюдаемых областях Вселенной выводы из математической обработки таких моделей должны подтверждаться наблюдениями (во всяком случае, не противоречить им), а также предсказывать новые явления, которые ранее не наблюдались. Из необозримого множества моделей, которые можно построить, лишь очень немногие могут удовлетворить этому критерию. В 70-х гг. 20 в. этому требованию наилучшим образом удовлетворяют разработанные на основе общей теории относительности однородные изотропные модели нестационарной горячей Вселенной.[xxxiv]

В данной работе получается, что формирование Вселенной созвучно с моделью нестационарной горячей Вселенной в которой первоначально формируются ФНП. Первоначально их границы проходят, с одной стороны, по внешним и внутренним поверхностям плоскостей ПНВЧ, а, с другой, по границам несамостоятельным телам пространства Ничто.

ФНП – единое тело

В этом момент, ФНП, как и фазовые пространства также можно рассматривать как однородные изотропные, а КЕП как неразличимые первичные элементы данных пространств являют собой материю в состоянии для-себя-бытия («абсолютное движение»[9]).

КЕП как абстрактное неопределяемое единичное место реального пространства, не позволяет говорить о дискретности конкретного ФНП. Основываясь на вышеприведенных логических определениях, как единство и противоположность двух моментов – единичности и непрерывности КЕП, принимаем аксиоматично, во-первых, факт их неделимости. И, во-вторых, наделяем их качествами абсолютной эластичности. Все вышеперечисленные свойства КЕП являются характеристическими[10], что соответствует математическому понятию «множество». Поэтому, как и фазовые пространства и ПНВЧ, ФНП КЕП, можно считать «несчетным множеством», которое также подходит под понятие единого тела, и, следовательно, все значения векторных величин, связанных с данным понятием, будут относительными[11].

Левое и правое Пастера, асимметрия и симметрия Кюри.

Рассмотренные нами характеристики КЕП как поляризации I и II в современной физике определяется понятием симметрии в виде M₀ и асимметрии в виде 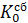.[xxxv] Таким образом, формирующиеся ФНП в зависимости от полярности могут быть отнесены либо к левой, либо правой системе координат. Поэтому, для корректного применения методологии векторного исчисления, необходимо пояснить понятия левая и правая система.  

Это явление было открыто для живых организмов – их тел – и для их проявлений в окружающем пространстве еще в 1848 г. Л. Пастером[xxxvi]. Пастер был одним из немногих, которые определен­но и твердо до конца жизни понимали значение найденного им своеобразного явления, резко отличавшего живые организмы в окружающем их мире[xxxvii]. Но он встретил многочисленные возражения, и долгое время его идеи не находили отклика. Через 46 лет после него П. Кюри[xxxviii] вернулся к найденным Пастером фактам и обобщениям и дал в связи с этим глубокое расширение учения о симметрии. Он дважды возвращался к этой проблеме: сперва в 1884 – 1894 гг., а затем вторично, незадолго до своей смерти (1906), не успев в последний раз ничего опубликовать из своих достижений[xxxix].

«Незадолго до трагической кончины в его дневнике отмечена замечательная фраза, что он нашел новые обобщения в учении о симметрии первостепенного значения[12]. Это не случайная запись, как мы видим сейчас, – можно предположить, что Кюри дейст­вительно унес с собой новые большие достижения, о которых мы сейчас можем только догадываться. Необходимо сюда направить научную работу. Наметки, которых рассмотрим ниже, дают возможность для научных исследований.

Кюри связывал асимметрию со своеобразной «неоднородно­стью», а симметрию, – с протяженностью. Асимметрия является как бы проявлением такой неоднородности, которая вообще не наблюдается. Мы вернемся к этому в свое время, а сейчас отметим, что основное положение, выдвинутое П. Кюри, можно рассматривать как один из основных принципов понимания логики науки о живой природе. Она заключается в том, что асимметрия может [вызываться] только причиной, которая сама уже обладает этой асимметрией. Будем называть в дальнейшем это положение принципом П. Кюри – Пастера.

В биографии П. Кюри, написанной его женой и дочерью[xl], приводится замечательное определение асимметрии, которое не встречается в его печатных произведениях и которое, очевидно, является развитием последних его размышлений. Он говорит, что «асимметрия есть état de l’espace – состояние пространства...»[xli], указав вместе с тем, что она есть проявление разнородности в полях симметрии. Условно будем считать, что на рис. 2, а изображены справа – правая, а слева – левая системы координат.