Момент инерции первых тел

Еще одной характеристикой, первых тел будет момент инерции[1], который отражает некую уравновешенность их динамических характеристик. В зависимости от соотношения m и ω момент инерции будет проявляться в поперечно-продольных колебаниях вращающейся массовой оболочки, отражающиеся на векторах МД^сб и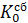. Так колебания вдоль оси вращения, связанные с вектором МД^сб, будут определятся как его продольный момент инерции –j, а поперечные колебания – как поперечный момент инерции – j_⊥. Для момента инерции вектора 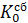– они поменяются местами. Таким образом, общий момент инерцииI_jбудет отражать моментальные векторные суммы обоих векторов МД^сб и.

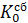Длительность существования первых тел

Таким образом, мы можем говорить о длительности существования телесных образований первых тел, и, следовательно, идентифицировать их физические характеристики, связанные с временным лагом[2].  При этом массовая оболочка так и поляризация, также являются неким компенсатором, поддерживающим постоянство соотношения ω и m.

Таким образом, с момента формирования телесных образований первых тел включилось время длительности их существования.

Кинематические связи, неделимость простых тел.

Таким образом, масса и поляризация влияют на физические характеристики поступательно-вращательного движения первых тел, и, следовательно, кроме геометрических величин будут изменять и физические величины, характеризующие их движение.

Учитывая еще максимально большую угловую скорость собственного вращения КЕП, и первых тел, ФНП можно рассматривать как механическую систему, в которой все связи механические[i] между первыми телами являются геометрическими (голономными)[ii]. Но в какой-то момент набора массы массовыми оболочками ними связи механические перестают быть голономными, а переходят в кинематические, которые налагают ограничения на его скорость вращения и поступательного движения. Этот момент можно рассматривать как границу существования первых тел реального пространства.

Таким образом, мы принимаем положение, что соотношение собственного движения и массы в первых телах соответствует состоянию ω ≫ m.  И, следовательно, они как КЕП будут неразличимые элементы несчетного множества ФНП, дискретность которых будет проявляться только на границах фазовых переходов, в т. ч. и на границах с ФНП КЕП. Поэтому, как и другие ФНП, пространства первых тел также подходит под понятие единое тело, и все значения индивидуальных векторных величин, связанных с данным понятием, будут относительными. Но в отличие от ФНП КЕП, благодаря наличию массовых оболочек ФНП первых тел могут сформировать собственное поступательно-вращение движение как единое тело.

Взаимодействие первых тел

Взаимодействие первых тел как с КЕП, так и между собой в момент БВ ведет к изменению соотношения m и ω. Если рассматривать единичные ТО, как механическую систему, связав их со временем t, и привязав m к кинетической энергии (Т), через I_j, а ω – к потенциальной энергии поляризации (П), то данную систему можно связать с каноническими уравнениями механики. Это позволит для находящихся в метастабильном состоянии ТО (t = 0) вычислять с помощью функции Гамильтона, можно находить все обобщенные координаты q_i и импульсы p_i как функции времени t и 2s постоянных (s – число степеней свободы системы), определяемых по начальным данным.[iii]

При этом общая энергия (Т и П) взаимодействующих тел «остаётся постоянной – она лишь перераспределяется» между этими телами, изменяя их соотношение m и ω. При этом меняются вектора МД^сб и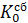 как по направлению, так и по величине, отражая возможное направления движения данных единичных элементов ТО.[iv]

Вышеприведенные рассуждения несколько расходятся с физическими характеристиками массы, введенные советским физиком В.А. Фоком[v] в фундаментальной работе математической физики «Теория пространства, времени и тяготения».

В этой работе, он, по сути, описывает не массу, как мы ее обозначили в данной работе, а первое тело, – конкретно – материальное тело[3].  В частности, он рассматривает тело, как состоящее из бесконечно малых величин, тензоров масс. Если понятие «тензор» (от лат. tensus – напряжённый, натянутый) рассматривать в первоначальном значении, введенного в теории упругости для обозначения малого растяжения и сжатия, возникающие при упругой деформации[vi], то эти характеристики хорошо согласуется с характеристиками не массы, а в целом первых тел. Это не противоречит учению о равновесном состоянии и движении, называемое в физике теорией упругости, и составляет «механику сплошных деформируемых тел».[vii] Таким образом, описание массы Фоком, совпадает с характеристиками первых тел.

Теория относительности и упругости в ФНП первых тел.

Интересно, что Фок, исследуя теорию упругости для абсолютно твердого тела на уровне релятивистской физики, в очередной раз столкнулся с тем, что на этом уровне исследования релятивистские формулировки теории упругости становятся не применимы. «...На релятивистской формулировке теории упругости мы здесь останавливаться не будем: Сделаем только одно замечание по во­просу о возможности применения понятия абсолютно твердого тела в теории относительности. В нерелятивистской механике понятие это вводится как абстракция, согласно которой форма и размеры тела не меняются под действием каких угодно сил. В частности, толчок, сообщенный в некоторый момент одному концу абсолютно твердого тела, немедленно приводит в движение и другой конец тела. На самом же деле для физического твердого тела волна от толчка рас­пространяется внутри тела со скоростью звука.

Поэтому принимаемая абстракция содержит в себе предположение, что скорость звука можно рассматривать, как бесконечно большую[viii]. Но очевидно, что если считать бесконечно большой скорость звука, то необходимо считать бесконечно большой и скорость света, так как она превышает скорость звука в сотни тысяч раз. Отсюда ясно, что абстракция, лежащая в основе понятия абсолютно твердого тела, применима только в нерелятивистской теории. В теории же относительности, основанной на учете факта конечной скорости распространения всякого рода действий, абстракция эта неизбежно приводит к противоречию. Следовательно, в теории относительности понятием абсолютного твердого тела пользоваться нельзя...»[ix].

Но данная теория, как можем пока предположить, хорошо подходит под понятие ФНП первых тел, где колебания, проявляющиеся на границах фазовых переходов, передаются по ФНП мгновенно, т. е. со скоростью максимально возможной. Таким образом, соотношение m и ω достигает некоего постоянства в конкретных ФНП простых тел как фактор их метастабильного состояния.

Резонансы

Согласно сегодняшним теоретическим выкладкам физиков, интенсивность БВ показывает практически мгновенное расширение Вселенной. «Последние данные указывают на то время, когда Вселенной было 10^–37 секунд отроду, а её температура достигала (в энергетическом эквиваленте) 10¹⁶ гигаэлектронвольт. По теории «Большого взрыва» эта чрезвычайно высокая энергия соответствует той, при которой становятся неотличимыми друг от друга три из четырёх фундаментальных взаимодействий — сильное, слабое и электромагнитное»[x].

В этот момент первые тела более всего согласуются с понятием «резонансов»[xi], но здесь, как можно предположить, они аннигилируют и распадаются в основном за счёт сверхсильных взаимодействий. Поэтому их времена жизни лежат в интервале меньше, чем 10^–22 – 10^–24 сек, и по порядку величины значительно меньше ядерного времени, а размеры «составляют порядка 10^–33 см»[xii].