3. Формирование центрального пространства Большого Взрыва

Форма пространства.

В процессе БВ, энергии и время действия потока неких внешних частиц было достаточно, чтобы в некой области пространства Ничто начало формироваться наше реальное пространство – Вселенная. Можно предположить, что ПНВЧ при распаде несамостоятельных тел при ударном воздействии, проникал в образующиеся области распада, формируя пространство две области БВ – внешнюю и внутреннюю. Процесс «проникновения» в «тело» пространства Ничто, а, следовательно, и анализ формы формирующегося пространства Вселенной, можно сравнивать с проявлениями аналогичных процессов при зарождении, скажем, многообразия форм живой и неживой природы.  Это, например, формирование цветов, фруктов, а также родников, бьющих из земли (см. рис. 5).

Рис. 5. Природные формы вокруг нас.

В этот момент активной фазы БВ происходило быстрое расширение границ реального пространства по внешним границам ПНВЧ. Можно предположить, исходя из формирования, например, яблока, что реальное пространство будет формироваться как совокупность двух тороидальных пространств, где тор внутренней области реального пространства, будет вписано в тор его внешней области. При этом форма формирующегося реального пространства будет походить на форму яблока (рис. 5, б и рис. 6).

Рис. 6. Разрез яблока. 1 – околоплодник, 2 – семенная ткань, 2 – наружная съедобная ткань.

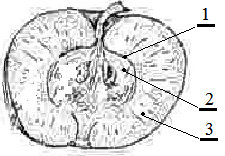В нем тонкий и твердый «околоплодник» олицетворяет некий поток внешних частиц, а во внешнюю и внутреннюю области реального пространства дифференцировалась съедобная ткань плода как наружная съедобная и семенная ткани. Внешнюю границу внешней области реального пространства с пространством Ничто, в этом случае, олицетворяет кожица яблока.[i]

Таким образом, форма пространства БВ, как внутренняя, так и внешняя будут представлять собой две тороидальные области, одна из которых меньшая вписана в другую. Это не противоречит одному из возможных геометрических изображений пространства, введенных Риманом. Он формулировал его «как непрерывной совокупности любых однородных объектов или явлений… введя понятие …пространства с любым законом измерения расстояний бесконечно малыми шагами (подобно измерению длины линии очень малым масштабом) … По Риману, пространство – это гладкое многообразие, в котором задан закон измерения расстояний, точнее длин, бесконечно малыми шагами, т. е. задаётся дифференциал длины дуги кривой как функция координат точки кривой и их дифференциалов. Это есть обобщение внутренней геометрии поверхностей, определённой Гауссом как учение о свойствах поверхностей, которые могут быть установлены измерением длин кривых на ней»[ii].

Такая форма, геометрии реального пространства, учитывая данные выше, логические определения, являясь органически связанным целым, представляют собой единую функцию Идеи, – развивать Разум, которая, как было показано выше, вписывается в математический аппарат теории аналитических функций. Учитывая необходимость длительного существования такого пространства и в то же время возможность его сворачивания в необходимый момент, мы можем говорить, что существование внутренней и внешней области реального пространства подчиняется двум главным аналитическим функциям, которые обладают свойством единственности, так называемым мероморфным функциям[1].

Исследования математической физики

Комфортным отображением этих аналитических функций в геометрии являются однолистные эллиптические образования. Примером такого отображения внутренних замкнутых областей согласно теореме Римана, являются и эллиптические поверхности[iii], изучение которых занимается математическая физика, например, в «Поверхностей теории»[iv], являющаяся частью «Дифференциальной геометрии»[v].

Исследование данных уравнений явилось основным предметом математической физики на рубеже XIXи XX веков. Одним из объектов исследований в дифференциальной геометрии являются семейство поверхностей, которые задаются посредством уравнений, например, (x– a)² + y² = 1, содержащие параметр метрики – a, т. е. комплексное число, отражающее два ряда сходящихся аналитический функций, которые, как можно предположить, отражают две тороидальные области реального пространства. Для нас они интересны тем, что данные уравнения определяет семейство окружностей радиуса 1 (r– на рис. 5, г) с центрами в точках (a, 0), т. е. как можно предположить и на оси центра круга тора[vi].

Это соответствует выкладкам математической физики о равновесии и  устойчивости фигур близких к эллипсоидам. Наиболее полные результаты были получены российскими ученными А.И. Ляпуновым[vii], для вращающейся неоднородной жидкости, которые были окончательно оформленными В.А Фоком в своей работе «Теория пространства и времени»[viii].

А.И. Ляпунов, исследуя уравнение Клеро[ix], которое стало камнем преткновения многих математиков, обратил внимания на противоречие содержащиеся в нем, которое основывалось на том, что данное уравнение пытались решать на основе предположения о том, что в основе строения тел являются шаровые или эллипсоидные формы. 

«Я нашел, – пишет он, – что эти последние предположения излишни и что существование решения уравнения, можно установить, предполагая лишь, что ρ постоянно убывает, когда a растет, и остается конечным при a = 0. Этого предположения вполне достаточно, чтобы установить, что рассматриваемое уравнение может иметь только одно решение, а также и для представления этого решения некоторым рядом...»[x].

Решению этого противоречия Ляпунов посвятил более двадцати лет. В последней известной мне работе он пишет: «Заметим, что нет необходимости прибегать к разложениям по шаровым функциям, – и, таким образом, можно обойти указанную нестрогость... <…> ...В дальнейшем изложении мы покажем, что вся теория может быть основана лишь на двух предположениях, а именно, что 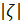 [2] – мало, и второе, что ζ является непрерывной функцией от a.

Кроме того, конечно, мы будем основываться на том, что речь идет о поверхности замкнутой и мало отличающейся от сферы...»[xi].

Возможно, данная работа была закончена перед его внезапной смертью... Поскольку к середине XX века было известно, что классическая теорема Пуанкаре, которая утверждает, «что единственное замкнутое многообразие всех касательных векторов к двумерной поверхности (M²) образует двумерное векторное расслоение (касательное расслоение) x² = TM². Векторное поле на M² определяет сечение в расслоении TM².M², допускающее гладкое касательное поле без особенностей на M², – тор (T²) …»[xii].

Что не противоречит и работам А.М. Ляпунова и В.А. Фока, где доказано, что устойчивое равновесие вращающегося упругого тела с неоднородной плотностью достигается в том случае, если тело имеет также, как и тор три плоскости симметрии.

Все вышеизложенное, дает основание предположить, что оптимальной формой, в которую формировались реального пространства БВ, могут быть тороидальными, где внутренний тор вписан во внешний (рис. 6 и 5, г).

Тороидальные криволинейные пространства

Следствием такого предположения являются и опыты исследования горячей плазмы в высокочастотных полях. «Как показали опыты П.Л. Капицы, в водороде и гелии при достаточно высоком давлении удаётся получить в ВЧ полях свободно парящий плазменный шнур с электронной температурой ~105 . Система допускает замыкание шнура в кольцо и наложение дополнительного продольного магнитного поля»[xiii]. В этом случае каждое комплексное число изображается соответствующей точкой сферы; последняя и названа сферой Римана[xiv].

Таким образом, одно из возможных геометрических изображений внутренней и внешней области тороидальных пространств БВ является Римана сфера, как совокупность комплексных чисел, где каждое комплексное число z = x + iy = r (cosφ + isinφ) = re^iφ изображается соответствующей точкой сферы декартовыми координатами x, y или полярными r, φ (Рис. 5. г).

Точка 0, лежащая в центре окружности поперечного сечения тороида изобразится при этом центром Римана сферы. Числа с одинаковым аргументом φ – const (лучи комплексной числовой плоскости) изобразятся меридианами AB, а числа с одинаковым модулем r = const (окружности комплексной числовой плоскости) – параллелями (широтами ED) Римана сферы (рис. 5г, 8а).

Интересно, что северному и южному полюсу AиB(рис. 5г, 8а) Римана сферы не соответствует никакая точка комплексной числовой плоскости.

В этом случае, векторное поле[xv] в любой его точке можно описывать функциями траектории криволинейного движения. Одной из таких функций, характеризующих изменение нормали поверхности (линии) будет градиент скалярного поля.

Таким образом, согласно определению МКД, отображающий его вектор будет лежать в плоскости перпендикулярной вектору МД, а его направление будет совпадать с касательной[xvi], лежащей в данной плоскости (рис. 2, а и рис. 3).

Формирование центральной области пространства Большого Взрыва.

О плазме

Обращаясь вновь к опытам исследования горячей плазмы П.Л. Капицей, можно видеть, что нейтральный ПНВЧ разделяющий полярные пространства КЕП, по структуре соответствует изотермической высокотемпературной плазме. Здесь мы имеем нейтральную среднюю часть в виде самого ПНВЧ и наружные и внутренние ФНП как «оболочки плазмы», полярных КЕП, которые «характеризуется кулоновскими силами притяжения и отталкивания»[xvii]. Таким образом, можно предположить о том, что энтропия полярных пространств в момент БВ в значениях температуры достигала значений высокотемпературной плазмы ~ 10⁶ – 10⁸ K и более. 

Современная физика описывает такие процессы горения как термоядерные процессы. Они идут при температурах в миллионы кельвинов, но и в этом состоянии плазмы, на ней имеются равновесные участки. Один из них, – «апериодический тип неустойчивости (в этих случаях отклонение от равновесия монотонно растет со временем). Такого типа неустойчивости характерны в основном для равновесных статических конфигураций плазмы, удерживаемой внутренними силами притяжения[xviii], в данном случае притяжением полярных КЕП. Это подходит под процессы, описываемые современной физикой, такие, как задачи об устойчивости плазмы (проблема Крускала–Шварцшильда)[xix].  

Для поддержания устойчивости такой плазмы необходима постоянная подпитка энергии, которая в процессе БВ поддерживается кинетической энергией ПНВЧ. При этом границы формирующихся двух функциональных торообразных областей «разбегаются» от центральной части БВ. Такой быстрый «разбег» границ можно характеризовать как «взрывная волна»[xx]. Идет лавинообразная экспансия формирующегося реального пространства в пространство Ничто. Это и дало нам возможность говорить об этом процессе как о «взрыве».

Центральная область Большого взрыва.

Таким образом, шел процесс формирования центральной области пространства БВ, которая в свою очередь состоит из двух полярных областей – внешней и внутренней, схематично представленная на рис. 7. Условно, по принятой поляризации КЕП будем считать, что внешняя область является функциональным пространством положительной поляризации, а внутренняя область – отрицательной. Поэтому, внутренняя область (рис. 7, 4) формировалась как внутренняя тороидальная область отрицательной поляризации, а, соответственно, внешняя – положительной (рис. 7, 3). Это не противоречит гипотезе, принятой выше, о том, что наличное бытие и природа, которая сформировалась во внешней тороидальной области, проявляется для нас через взаимодействие материи в состоянии для-себя-бытия и в-себе-бытия.

Таким образом, в процессе БВ формирующиеся полярные тороидальные ФНП можно рассматривать, как основу асимметрии пространства. Это соответствует и принципу П. Кюри – Пастера, – в основе формирования пространств Вселенной лежит асимметрия пространств БВ в части зарядового сопряжения[3].

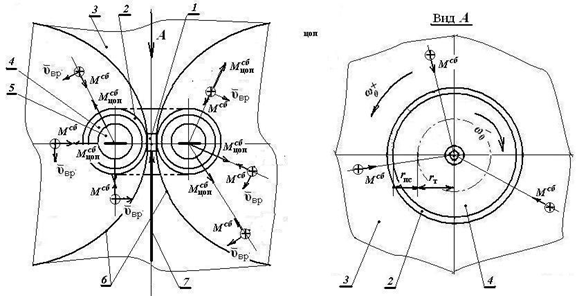
Рис. 7. Схема направления векторов взаимодействия с ЦОП БВ. 1 – Область начала и завершения воздействия потока неких внешних частиц (ПНВЧ); 2 – Нейтральная оболочка из ПНВЧ; 3 – Внешняя область ЦОП БВ; 4 – Внутренняя область ЦОП БВ; 5 – знак отрицательной поляризации ЦОП: 6 – Формирующиеся границы пространства БВ; 7 – Направление воздействия ПНВЧ.

Центр отрицательной поляризации (ЦОП)

Внутренняя область по радиусу r_τ (см. рис. 7 вид A) формировалась как поле КЕП отрицательной полярности. Границей этих двух полярных областей является также сформировавшийся в тор нейтральный ПНВЧ. Можно предположить, что сформированное внутреннее ФНП, являет собой единое тело. Это позволяет говорить о нём, как центре отрицательной поляризации – ЦОП (рис. 7, 5).

В то же время внешнюю область БВ можно рассматривать как систему отдельных ФНП, где идут постоянные процессы формирования и аннигиляции телесных образований, в большинстве своем положительной поляризации. Их МД будут направлены к ЦОП. Соответственно, МД всех отрицательно поляризованных образований будут направлены в противоположную сторону.

Можно предположить, что внешняя область будет несоизмерима по размерам с внутренней. Поэтому по отношению к ней ЦОП БВ в масштабах Вселенной можно рассматривать как точечный полюс отрицательной полярности.

Внутренняя область тора ЦОП

Можно предположить, что после окончательного формирования центральной области, процесс БВ закончится, и начнется процесс охлаждения сформированного пространства. В процессе охлаждения внутренней области ЦОП, в ней будут преобладать КЕП отрицательной поляризации, например, изотопов ¹²Cотрицательно поляризации, которые при температуре БВ находились в газообразном состоянии. При быстром охлаждении, как можно предположить, они перешли в жидкий раствор с металлической структурой α-железа или α-феррита. Вполне возможен переход его и в промежуточное положение между кристаллом и квантовой жидкостью, поскольку «у квантовых жидкостей эти свойства полностью разрушают кристаллическую структуру, а у квантовых кристаллов волновые свойства атомов, сохраняя выделенность узлов кристаллической решётки, допускают их перемещение (с узла на узел)»[xxi].

При этом, согласно «Нётер теореме[xxii], каждому преобразованию симметрии, характеризуемому одним непрерывно изменяющимся параметром, соответствует величина, которая сохраняется (не меняется со временем) для системы, обладающей этой симметрией. Из симметрии физических законов относительно сдвига замкнутой системы в пространстве, поворота её как целого и изменения начала отсчёта времени следуют соответственно законы сохранения импульса, момента количества движения и энергии…»[xxiii]. Таким образом, можно предположить, что поляризация замкнутой внутренней области ЦОП будет сохраняться бесконечно долго, пока существует оболочка ПНВЧ.

Внешняя область тора ЦОП

Асимметрия ЦО внешних пространств, в который они описывается волновой функцией, справедлив суперпозиции принцип[4]. Если дискретность системы рассматривать относительно пространственной инверсии внешних и внутренних пространств ЦОП, то в этом случае законы сохранения, например, можно рассматривать на примере пространственной чётности[5]. «Действительно, пусть ψ₁ – волновая функция, описывающая какого-либо состояние системы, а ψ₂ – волновая функция системы, получающаяся в результате пространств. инверсии (символически: ψ₂ = 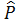ψ₁, где 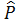– оператор пространств, инверсии). Тогда, если существует симметрия относительно пространственной инверсии, ψ₂ является одним из возможных состояний системы и, согласно принципу суперпозиции, возможными состояниями системы (относительно ПНВЧ (ψ_a) – мое) являются суперпозиции ψ₁ и ψ₂ симметричная комбинация ψ_a = ψ₁ + ψ₂… При преобразованиях инверсии состояние ψ_aне меняется (т. к. 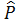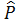ψ_a = ψ₁+ 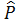ψ₂ = ψ₁ + ψ₂ = ψ_a) … В данном «случае говорят, что пространственная чётность системы внутренних полей положительна (+1) ... Если волновая функция системы задаётся с помощью величин, которые не меняются при пространственной инверсии (таких, например, как МКД и энергия[6]), то вполне определённое значение будет иметь и чётность системы. Система будет находиться в состоянии либо с положительной, либо с отрицательной чётностью (причём переходы из одного состояния в другое под действием сил, симметричных относительно пространств. инверсии, абсолютно запрещены).

Аналогично, из симметрии относительно зарядового сопряжения и комбинированной инверсии следует существование зарядовой чётности (С-чётности) и комбинированной чётности (СР-чётности). Эти величины, однако, могут служить характеристикой только для абсолютно нейтральных (обладающих нулевыми значениями всех зарядов) частиц или систем…»[xxiv], т. е. ПНВЧ.

Действительно, во внешней области БВ где процессы образования и распада телесных образований продолжаются и после окончания БВ преобладают изотопы ¹³C положительной поляризации.

Таким образом, возможны формирование телесных образований как со структурой ферромагнетиков положительной поляризации, так же и со структурой парамагнетиков. При этом, еще при высоких температурах БВ, т. е. в процессах полукоксования[xxv], взаимодействие распадающихся несамостоятельных тел, при преобладающих КЕП положительной поляризации, привели к образованию многочисленных телесных образований с различным соотношением m и ω преимущественно положительной полярности. В нашей гипотезе, это различные газообразные элементы как самого углерода, так и кислорода, водорода, азота и др.[xxvi]

Расслоение внешних ФНП

С удалением процесса БВ от ЦОП, внешние пространства будут охлаждаться до температур близких к нулевой, способствуя формированию ФНП и РП с различными соотношениями m и ω. Границы фазовых переходов делают их похожими на «слои», а сами фазовые переходы, – на «струны[xxvii]».

Данное расслоение можно представить, как объединение «слоев» РП во внешнем пространстве центральной области (ПЦО) БВ – РП∈ПЦО, параметризованных точками базы и «склеенных» фазовыми переходами (или более обще – топологией пространства ПЦО). Группа пространств ПЦО называется структурной группой расслоения. Базой расслоения служит ЦОП, а слоем – единичное РП как материальное тело.[xxviii] Как несчетное множество каждое РП является векторным пространством.

Гравитация 

В центральной области БВ взаимодействие МД^сб внешних ФНП и 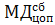 можно будет практически воспринимать, как действие единичных векторов 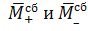. Но если величина 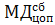 будет постоянной, то величина МД^сб ФНП нет, поскольку она будет, как было отмечено выше, уменьшаться с удалением от ЦОП. В современной теории релятивистской астрофизики[xxix] внешнее единое поле РП более всего подходит под классификацию гравитационного поля вокруг сильно сжатой массы. Это позволяет систему взаимодействия ЦОП и внешних полей центральной области БВ определять понятиемгравитации[7]. 

Область пространства, в которой гравитация доминирует над притяжением всех других небесных тел, хорошо ложится понятие «сфера действия тяготения»[xxx].

Следовательно, гравитация будет убывать при удалении от ЦОП. В центральной области БВ величины 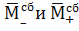 достигают максимальной величины, и на границе оболочки ПНВЧ достигают величины тяжести.

Таким образом, единичный вектор любой точки пространств центральной внешней области БВ будет в т. ч. отражать как скаляр, изменение распределения массы, сходящихся к внешней границе тора ЦО БВ. Поэтому градиент, дивергенция и вихрь скалярного поля масс будет основным дифференциальным оператором поля гравитации.[xxxi]

Тяжесть.

Таким образом, уже в процессе БВ формировались полярные пространства, в которых заложен механизм сворачивания Вселенной, основанный на возможности аннигиляция КЕП внутреннего и внешнего пространств. Это согласуется с понятием «тяжесть», даваемое Гегелем, «как системы взаимодействующих пространств, образующих «для-себя-сущее многое, как всеобщее для-себя-бытие, находящееся одновременно в и вне его, – это есть тяжесть»[xxxii]. Основным элементом поддерживающим, поддерживающим метастабильное длительное существования пространств внутренней и внешней области БВ, является оболочка ПНВЧ (рис. 7, 2).[xxxiii] Такое образование мы наделим понятием «система тяжести».

Соленоид центральной области Большого Взрыва.

Систему полей ФНП внешней центральной области пространств БВ с внутренним пространством ЦОП, как полюсом отрицательной поляризации, можно отнести к структуре закрытых несчетных множеств. Это позволяет нам опираться на теорию слабых и электромагнитных взаимодействий[xxxiv], которую можно будет применять при описании процессов взаимодействия таких полей и телесных образований, формирующихся в них.

Как внутренняя, так и внешняя области пространства БВ получили импульс действия ПНВЧ – mυ^вн (рис. 2, а), а также потенциальную энергию в виде векторов поступательного движения (рис. 7). Как можно предположить, векторная сумма данных векторов подходит под понятие вихря (или ротора) поля, который представляет собой векторную характеристику «вращательной составляющей» поля (его «скручивание»). Согласно теории «Векторного анализа»[xxxv] векторное потенциальное поле называется соленоидальным, или трубчатым, если это поле представляет собой вихрь некоторого поля[8], которое называется векторным потенциалом данного поля.

Это не противоречит нашей гипотезе, где центральная область БВ формируется как соленоид, где «одновитковой катушкой индуктивности» является тор потока неких внешних частиц (рис. 7.2), а «током» будем считать поле КЕП внутри тора (рис. 7.4). Магнитным полем, проходящем поверх «катушки», являются векторные поля полярности I РП внешних пространств БВ (рис. 7.3).  Для того чтобы оно было соленоидальным[9], необходимо и достаточно обращение в нуль дивергенции (расхождение)[10] векторов данного поля, т. е. в нашем случае div 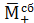 → 0.

Как было показано выше, внешняя область пространства БВ, состоящее в том числе из эфира Аристотеля, представляет собой скалярное поле плотности масс РП. При этом сумма векторов, подходит под понятие вихря (или ротора) поля, который представляет собой векторную характеристику «вращательной составляющей» поля (его «скручивание»). В такую потенциальную воронку как бы «втягиваются» пространства эфира Аристотеля по направлению действия ПНВЧ (рис. 7, 7).  

Данное втягивание подразумевает поступательное-вращательное движение РП как единого тела, которое возможно только если они могут формировать собственный импульса действия – mυ. Что это возможно, подтвердили астрофизики. Так «международный коллектив астрофизиков сообщил об обнаружении рентгеновских ветров со скоростью 3000 км/сек вблизи черной дыры… <…> …По данным Европейского космического агентства, двоичная система, как v404 Лебедя, которая находится в 10 раз больше массы солнца, как правило, собирает материал из межзвездного пространства на диске, где она нагревается до спирали в черную дыру…»[xxxvi].

При втягивании в воронку, повышается давление между РП, что увеличивает взаимодействие между легкими частицами по границам ФНП. Это ведет к увеличению массы частиц и… их охлаждению. При этом происходит поперечное «сужение» ФНП и… в последующем «слияние» в одно пространство, где уже преобладает масса, что может говорить об возрастании ИД потока или стока, а, следовательно, и к увеличению скорости поступательно-вращательного движения уже единого потока. Нельзя исключать возможность попадания в воронку отдельных элементов несамостоятельных тел.

Дальнейшее резкое сужение воронки приводит к еще большему увеличению внутреннего давления между элементами самого потока. В нем начинаются интенсивные процессы аннигиляции телесных образований, и преобразование их в поток жидкого раствора кристаллов с вкраплением в него «лишних» КЕП₊. Поляризация потока падает практически до нуля, что действительно подходит под описания «гравитационного коллапса»[xxxvii]. Можно предположить, во-первых, что внутренне давление жидкого раствора в центральной части сравнится с внутренним давление ПНВЧ оболочки тора. В процессе выравнивания давлений, во-первых, жидкий раствор начнет «терять» жидкие кристаллы «восполняя» потери ПНВЧ ЦОП, потерянные им в своем поступательно-вращательном движении от взаимодействия с КЕП внутреннего и внешнего полярных пространств БВ.

Это не противоречит неразрывности уравнения в гидродинамике, отражающий закон сохранения массы для любого объёма движущейся жидкости (газа), когда жидкость уже не сжимаема. Согласно закону, в центральной области ЦОП где площадь поперечного сечения S можно считать постоянной, будет наблюдаться закон постоянства расхода ρSυ = const.[xxxviii] Следовательно, во-вторых, оставшаяся жидкая смесь «выносится» с большой скоростью в «раскручивающуюся» воронку – слив.

Таким образом, центральная область пространства БВ функционирует как соленоид с двумя потенциальными полями. Соленоид состоит из тора оболочки ПНВЧ с радиусом r_пс, внутреннего отрицательно поляризованного поля (ЦОП) с внутренним радиусом r_τ(рис. 7, А). И внешних потенциальных пространств БВ положительной поляризации. Это не противоречит нашему представлению о форме реального пространства, сделанное на основе образований живой природы (рис. 5, а – в, 6).

Черная дыра, ветер, сферы и струны.

В процессе возгонки расширяющегося горла воронки слива происходит преобразование жидкой смеси в газообразную. Начинаются формироваться РП с разными соотношениями ω и m, что сопровождается их интенсивным охлаждением. Дивергенция начинает увеличиваться – div a > 0, – исход, что можно связать с наличием некоего ветра. «Ветер, который берет свое начало в космической черной дыре похож на аккреционный[11] диск, … несмотря на яркий и очень жесткий, с постоянными изменениями в яркости и выбрасыванием массы в виде струй взрыв…»[xxxix].

Пространство воронки центральной области ЦОП в современной физике более всего подходит под описание и Кёрра пространства-времени[xl], которое связано с процессами происходящих в так называемой черной дыре[12].

Но в настоящей работе необходимо несколько по-иному расставить акценты. Возвращаясь к теории расслоения пространств, можно сказать о том, что данные пространства, которые как бы выбрасываются из центральной области ЦОП, трактуются в теории расслоения как пучки сфер. Это наиболее полно отражает структуру РП внешней области ЦОП. А вот проявляющаяся для нас в виде реликтового излучения граница фазовых переходов между РП – струны, с одной стороны, как бы сходят в черную дыру, а с другой исходят из неё, образуя «потоки» излучения. Интересно, что исход в современной астрономии хорошо подходит под описание Сейферта галактики[13].

Современная же физика трактует понятие «черная дыра» как – космический объект, возникающий в результате сжатия телесных образований гравитационными силами, на основании общей теории относительности (ОТО).

«В основе общей теории относительности лежит экспериментальный факт равенства инерциальной массы (входящей во второй закон Ньютона) и гравитационной массы (входящей в закон тяготения) для любого тела, ведущий к эквивалентности принципу. Равенство инерционной и гравитационной масс проявляется в том, что движение тела в поле тяготения не зависит от его массы…»[xli]

Но даже если рассматривать собственное вращение ω легких частиц как инерционную массу, то равенство ω и m лишь частный случай, о котором будет идти речь ниже. Тем не менее движение тела в векторном поле гравитации будет существенно зависеть как от ω, так и m. А гравитационный коллапс, действительно происходит, но не от быстрого сжатия звезды, и не на «поздних стадиях эволюции» звёзд. Но, как описано выше, переходом ω в m и формированием инерционного жидкого раствора, который, как показано выше, пополняет энергию нейтральной оболочки тора ЦОП, что после окончания БВ служит как механизм, поддерживающий метастабильное равновесие данной оболочки.

Таким образом, источником энергии формирующегося соленоида в таких процессах, можно считать постоянство потенциальной энергии ЦОП и процессы, происходящие во внешнем пространстве БВ, где постоянная экспансия пространства Вселенной в пространство Ничто, и как следствие постоянный распад последнего на несамостоятельные тела, которые являются поставщиками потенциальной энергии движения. Таким образом поддерживается метастабильное состояние Вселенной.

Прецессия.

Вектора поляризации I внутреннего и внешних пространств области БВ как единых тел отражают собственное вращательное движения своих элементов – 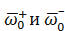и соответственно. Они будут всегда направлены по касательной к окружности горизонтального сечения тора ЦОП (рис. 7, А). Как можно предположить, вблизи границ ЦОП градиенты векторов 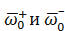 соразмерны, но направлены в разные стороны. В этом случае они, действуя как пара сил (см. рис. 1, пара сил), они создают поперечные колебания вертикальной оси тора z (рис. 10, б. 7) с центом в точке пересечения xи z. Данные колебания будут отклонять собственную ось тора от оси z. Физика классифицирует такое движение вертикальной оси как регулярная прецессия[xlii].

Пространственно-временной континуум

Отметим, что с окончательным формированием центральной области БВ, в котором определилось собственная система тяжести, обеспечивающая ей метастабильное состояние. В этот момент заканчивается второй период инфляции. Время из состояния «в-себе-бытие» (длящееся), перешло в состояние конечного «бытия-для-нас». С этого момента мы можем сказать, что время стало неотъемлемым атрибутом пространства БВ как единого тела, что позволяет ввести для него понятие «пространственно-временной континуум» (ПВК) Вселенной.

ФНП внутренней и внешней области ЦОП как совокупность количественных пространств однородных элементов, можно рассматривать как сепарабельные пространства[xliii] (от лат. separabilis – отделимый), каждое их которые «возможно представить элементом пространства как предел последовательности элементов из счётного множества. Их можно смотреть с точки зрения специальной теории относительности. Последняя утверждает, что многообразие пространств ФНП БВ есть псевдоевклидовы пространства, т. е. такие, в которых роль движений играют преобразования, сохраняющие квадратичную форму x²+ y²+ z²– k²t² (где k– коэффициент неравномерности скорости времени). Точнее, это есть пространства с группой преобразований, сохраняющих указанную квадратичную форму в единой инерционной системе.

Согласно же общей теории относительности, многообразие ФНП БВ неоднородны и лишь в каждой бесконечно малой области сводится к псевдоевклидову, т. е. они есть пространства картановского[xliv] типа. Само понятие о пространствах такого типа появилось после теории относительности, и было развито под её прямым влиянием.

В самой математике положение и роль геометрии определяются, прежде всего, тем, что через неё в математику вводилась непрерывность. Математика как наука о формах действительности сталкивается, прежде всего, с двумя общими формами: дискретностью[14] и непрерывностью.

Об этом же двести лет назад писал Гегель. «Если мы поставим точку, то мы прервем его (пространство – мое), но само пространство благодаря этому отнюдь не прерывается. Точка имеет смысл лишь постольку, поскольку она пространственна, следовательно, она внешняя по отношению к себе и к другой точке. «Здесь» само в свою очередь обладает неким верхом, низом, правой, левой стороной. Настоящей точкой было бы то, что внешне лишь в отношении к другим, а не внешне в самом себе, но таковой нет, потому что никакое «здесь» не является чем-то последним. (Как бы далеко я ни отодвигал звезду, я могу все же пойти дальше) …»[xlv]